Description Logics.
DL Knowledge Base
- decidable fragments of first-order logic allowing reasoning about complex logical axioms over unary and binary predicates.
- BC, DL = TBOX (intentional part) + ABOX (assertional part).
- In DL, classes are called concepts and properties are called roles.
- Tbox T is a set of terminological axioms which state inclusions or
equivalences between concepts and roles
- Abox A is a set of assertions indicating the memberships of individuals
to concepts and the memberships to roles for pairs of individuals.
The ingredients for building a DL knowledge base are:
- a vocabulary composed of a set C of atomic concepts (A, B...), a set R of atomic roles (P,Q...), and a set O of individuals (a, b, c ...),
- a set of constructs used to construct complex concepts and roles from atomic concepts and roles,
- a language of axioms that can be stated to constrain vocabulary to express domain constraints.
o Simple inclusion axioms: are inclusion relations between atomic concepts or roles, which correspond to the subClassOf and subPropertyOf relations of RDFS.
o Axiom of General Inclusion: relations of general inclusion between complex concepts (called GCI) or of inclusion between complex roles
Examples: complex concepts
- Student ∩ Researcher is a complex concept constructed from the two atomic concepts Student and Researcher using the conjunction construction (which is denoted owl: intersectionOf in OWL).
- Student ∩ ∀ RegisteredTo.MathCourse is a complex concept to represent students who are exactly enrolled in math courses only
- Student ∩ ∃ RegisteredTo.MathCourse is a complex concept representing students registered in at least one mathematics course
Examples: axioms of inclusion and equivalence
- Axioms of inclusion:
•MathCourse ⊆ Course
•LateRegisteredTo ⊆ RegisteredTo
- Axioms of general inclusion :
•PhDStudent ⊆ Student ∩ Researcher
•MathStudent⊆ Student ∩ ∃ RegisteredTo.MathCourse
•∃ TeachesTo.Undergrad ⊆ Professor ∪ Lecturer
- Axioms of equivalence:
•CSStudent≡ Student ∩ ∀ RegisteredTo.ComputerSienceCourse
The semantics of a DL is based on standard logical semantics in terms of FOL interpretations of individuals as constants, concepts as subsets, and roles as binary relationships.
Reasoning problems taken into account in DL
Satisfaction checking: given a knowledge base DL 𝒦 = (T, 𝒜), is 𝒦 satisfiable?
Subsumption checking: given a Tbox T and two concept expressions C and D, T ⊨ C ⊆ D?
Instance Checking: Given a knowledge base DL 𝒦 = (T, 𝒜), e is an individual and C is a concept expression, does 𝒦 ⊨ C(e)?
Query Answering: Given a knowledge base DL 𝒦 = (T, 𝒜) and a conceptual expression C, find the set of individuals e such that 𝒦 ⊨ C(e)
For DLs with full negation: instance checking and subsumption checking can be reduced to (un)satisfiability checking.
• T ⊨ C ⊑ D ⇔ (T, {(C ⊓ ¬D) (a)}) is unsatisfiable.
• (T, A) ⊨ C (e) ⇔ (T, A ∪ {¬C (e)}) is not satisfiable.
Description Logics Family.
ALC. 
o ALC Tbox is a set of simple or general inclusion axioms.
o ALC Abox is a set of assertion C(a) or R(a,b
Reasoning with ALC : A tableau-based satisfiability algorithm
Example: we want to know whether ∃R.A⊓ ∃R.B ⊆ ∃R.(A⊓B)
1. Transform to unsatisfiablity problem C=∃R.A⊓ ∃R.B ⊓ ¬(∃R.(A⊓B))
2. Push negation inside using Morgan rules
∃R.A⊓ ∃R.B ⊓ ∀R.¬A⊔¬B)
3. Try to construct a finite interpretation I such that CI≠∅
- There must exist an individual b ∈∆I such that b ∈CI
- Generate such an individual b ∈∆I and impose the constraint b∈CI
b∈CI means b ∈ ∃R.A and b∈∃R.B and b ∈ ∀R.¬A⊔¬B. Therefore, we have
b ∈ ∃R.A means there exist c ∈ ∆I and c≠b such that c ∈ AI and R(b,c).
b∈∃R.B means there exist d ∈ ∆I and d≠c and d≠b such that d ∈ BI and R(b,d).
b ∈ ∀R.¬A⊔¬B means c ∈ ¬AI or c ∈ ¬BI. or c ∈ AI. so c ∈ ¬BI
also b ∈ ∀R.¬A⊔¬B means d ∈ ¬AI or d ∈ ¬BI. or d ∈ BI.so d ∈ ¬AI.
Finaly, we construct an interpretation I on ∆I ={b,c,d} such that AI={c}, BI={d}, R={(b,c),(b;d)}
As a result, ∃R.A⊓ ∃R.B ⊆ ∃R.(A⊓B).
Tableau based reasoning Algorithm.
Rule ⊓:
Condition: A contain (C ⊓ D) (a) but not both C (a) and D (a)
Action: add A ′ = A ∪ {C (a), D (a)}
Rule ⊔:
Condition: A contain (C ⊔ D) (a) but neither C (a) nor D (a)
Action: add A ′ = A ∪ {C (a)} and A ′ ′ = A ∪ {D (a)}
Rule ∃:
Condition: A conain (∃R.C) (a) But there is no c such that {R (a, c), C (c)} ⊆ A
Action: add A ′ = A ∪ {R (a, b), C (b)} where b is a new individual
Rule ∀:
Condition: A contain (∀R.C) (a) and R (a, b) but not C (b)
Action: Add A ′ = A ∪ {C (b)}
Expressivity and Reasoning Complexity
ALC :
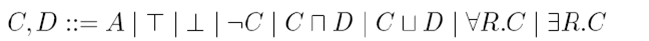
satisfiability , subsomption and instance checking are EXPTIME-complete
FL: conjunction C1 ⊓ C2, roles co-restriction ∀R.C and ∃R
◮ For Tbox without GCI, subsomption checking is polynomiale
◮ For Tbox with GCI (and CI), subsomption checking is co-NP complète (coNP contains problems that have a polynomial time verification for “no” answers).
EL: conjunctions C1 ⊓ C2 and existential restrictions on roles ∃R.C
◮ subsomption checking is polynomial even for Tbox with GCI.
FLE: conjunction C1 ⊓ C2, co-restrictions on roles ∀R.C and existential Restrictions on roles ∃R.C
DL-LITE: a good compromise, specially designed for garantir query answering modulo
ontologies be
polynomial in data complexity.
A is an atomic concept and R is a rôle (atomic), two types of concepts:
- B is a basic concept. It is either an atomic concept or complex of the following forms ∃R and ∃R-.
- C is a complex concept.
- Tbox DL-Lite : B ⊆ C and(funct R), (funct R-)
Query answering modulo DL-Lite
Query answering modulo DL-Lite is different from query answering from RDFS:
Incompletness. RDFS rules (axioms ) are safes , allowing an ascendent algorithm (Saturation). DL-LITE axioms might not be safes. An ascendante approach might results to incomplets facts.
Example :
From the fact Professeur (Ahmed) and the axiom Professor ⊆∃TeachesIn which means ∀X(Professor(X))⟹∃Y(TeachesIn(X,Y))) , we infer that there are one or more courses that Ahmed teaches. In other words, we know that there is a fact of the form TeachesIn(Ahmed, y) that is true but we do not know the value of y.
Therefore, we will have to use a top-down approach to evaluate queries which is more appropriate than the bottom-up approach.
Query answering modulo DL-Lite in 3 steps:
- Query rewriting: translate the original query q into a set of queries qi.
- Evaluate the qi over the Abox.
- For every Abox A such that (T ∪A) is satisfiable:
Answer (q0, T ∪A) = ∪ Answer (qi, A)
Query rewriting:
translate the original query q into a set of queries qi.
Translating Rules of GCI (right to left) :

where _ indicates a new variable that appears only once.
Basically, we get the rewritten qi by applying the rules and unifying the variables in whatever way possible.
Useful materials:

