المحاضرة 09+التطبيق09

مثال 02: سعر الصرف الرسمي للدينار مقابل الدولار الامريكي (1960-2022)، طبيعة البيانات سنوية.

رابط المعطيات:

https://data.worldbank.org/indicator/PA.NUS.FCRF?locations=DZ

نفس المراحل السابقة لوضع المعطيات في ملف Excel.

لنحصل على قاعدة المعطيات التي أسميناه "data3":

نقوم باستيراد قاعدة المعطيات: علما أن السنوات طبيعتها رقمية (طريقة الاستيراد تم التطرق لها سابقا):

التعريف بالسلسلة الزمنية:

edd<-ts(data3$edd,start=1960)

أ- التمثيل البياني للسلسلة الزمنية:

plot(edd)

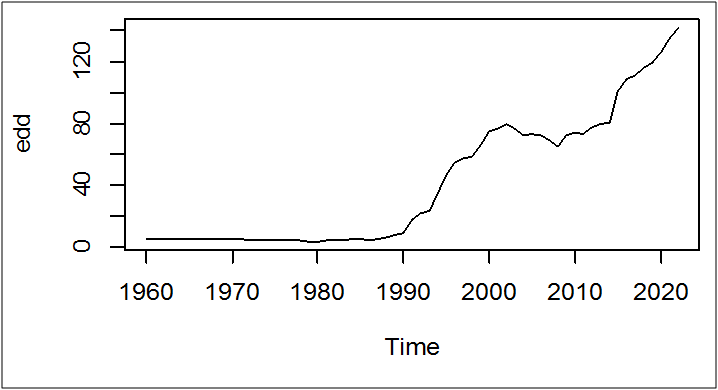
الملاحظ من الشكل البياني ما يلي:

-          وجود اتجاه عام تصاعدي: احتمال كبير أن السلسلة غير مستقرة

-          عدم وجود نقاط شاذة أو تغيرات هيكلية تؤثر بشكل واضح في نمط السلسلة.

ب- دراسة استقرارية السلسلة الزمنية:

بشكل عام اختبارات الاستقرارية مبنية على الفرضيتين:

H0: عدم الاستقرارية (Nonstationarity)

H1: وجود استقرارية (stationarity) 

نحتاج حزمة (tseries):

library(tseries)

adf.test(edd)

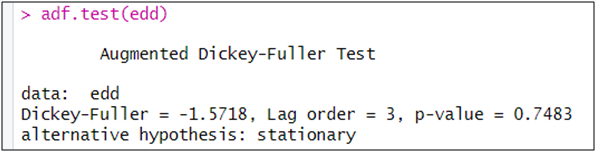
الملاحظ أن اختبار ADF بين أن السلسلة edd غير مستقرة، و ذلك من خلال عدم رفض الفرضية الصفرية و ذلك كون أن الاحتمال (p-value) أكبر من 5 بالمائة.

خلاصة:بين الاختبار أن السلسلة edd غير مستقرة، و عليه يجب جعلها مستقرة حتى يمكن نمذجتها باستخدام نموذج ARIMA.

يمكن أن نعمل لها الفروق من الدرجة الأولى و نعيد اختبارات الاستقرارية:

dedd<-diff(edd,differences = 1)

plot(dedd)

الملاحظ أن سلسلة الفروق يمكن أن تكون مستقرة.

adf.test(dedd)

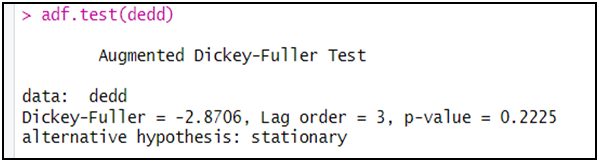
الملاحظ أن اختبار ADF بين أن السلسلة dedd غير مستقرة، و ذلك من خلال عدم رفض الفرضية الصفرية و ذلك كون أن الاحتمال (p-value) أكبر  من 5 بالمائة.

يمكن التأكد باستخدام اختبار ثاني:

pp.test(dedd)

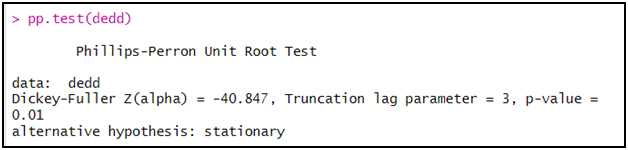
الملاحظ أن اختبار PP بين أن السلسلة dedd مستقرة، و ذلك من خلال رفض الفرضية الصفرية و ذلك كون أن الاحتمال (p-value) أقل من 5 بالمائة.

يمكن الاستعانة باختبار KPSS للفصل في هذا التناقض بين ADF و PP، و اختبار KPSS مبني على الفرضيتين التاليتين (عكس بقية اختبارات جذر الوحدة):

H0: وجود استقرارية (stationarity)

H1: عدم الاستقرارية (Nonstationarity)

kpss.test(dedd)

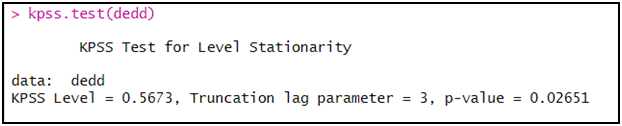
الملاحظ أن اختبار KPSS بين أن السلسلة dedd غير مستقرة، و ذلك من خلال رفض الفرضية الصفرية و ذلك كون أن الاحتمال (p-value) أقل من 5 بالمائة.

خلاصة:بينت الاختبارات أن السلسلة dedd غير مستقرة، يمكن أن نعمل لها الفروق من الدرجة الثانية و نعيد اختبارات الاستقرارية:

ddedd<-diff(dedd,differences = 1)

plot(ddedd)

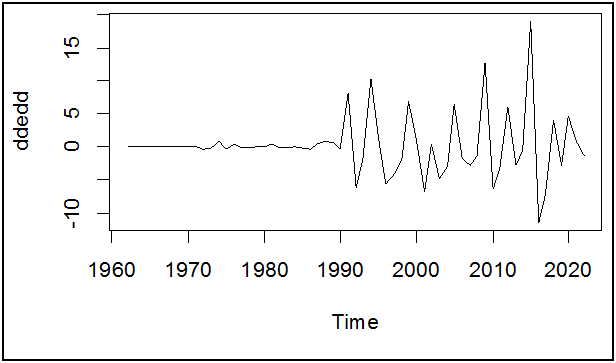
الملاحظ أن سلسلة الفروق يمكن أن تكون مستقرة.

adf.test(ddedd)

الملاحظ أن اختبار ADF بين أن السلسلة ddedd مستقرة، و ذلك من خلال رفض الفرضية الصفرية و ذلك كون أن الاحتمال (p-value) أقل  من 5 بالمائة.

يمكن التأكد باستخدام اختبار ثاني:

pp.test(ddedd)

الملاحظ أن اختبار PP بين أن السلسلة ddedd مستقرة، و ذلك من خلال رفض الفرضية الصفرية و ذلك كون أن الاحتمال (p-value) أقل من 5 بالمائة.

الخلاصة: السلسلة ddedd مستقرة و بالتالي يمكن نمذجتها باستخدام نموذج ARIMA، و بما أن السلسلة المدروسة تطلبت الفرق الثاني لتستقر فإن النموذج يكون من الشكل ARIMA(p,2,q).

ج- التأكد من أن السلسلة المستقرة ليست سحابة بيضاء:

ذكرنا سابقا أن كل سحابة بيضاء هي سلسلة مستقرة بينما ليس كل سلسلة مستقرة هي سحابة بيضاء، نلاحظ من الشكل السابق للسلسلة ddedd ذات المتوسط المقارب للصفر أنه يمكن أن تكون السلسلة الأخيرة سحابة بيضاء، يمكن التأكد باستعمال اختبار Box–Pierce or Ljung–Box Test Statistic، حيث الاختباران يفحصان الفرضيتان:

H0: عدم وجود ارتباط ذاتي

H1: وجود ارتباط ذاتي

بما أن حجم العينة هو 61 مشاهدة (لأنها سلسلة فروق طرحت منها مشاهدتين) سنختار حسب قاعدة Rob J Hyndman درجة التأخير lag المثلى هي 13.

Box.test(ddedd, lag = 13)

بما أن الاحتمال (p-value) أقل من 5 بالمائة فإننا نرفض الفرضية الصفرية

و القائلة بعدم وجود ارتباط ذاتي للسلسلة المدروسة و نقبل الفرضية البديلة،

.إذا السلسلة الزمنية ddedd ليست سحابة بيضاء

ج- اختيار نموذج ARIMA الملائم:

و يكون ذلك بتحديد درجتي p و q، و يكون ذلك عن طريق دالة الارتباط الذاتي الكلي و دالة الارتباط الذاتي الجزئي،

- تحديد درجة إبطاء MA(q): يكون ذالك من خلال دالة الارتباط الذاتي الكلي ACF، بالشكل التالي:

acf(ddedd,lag.max=13)

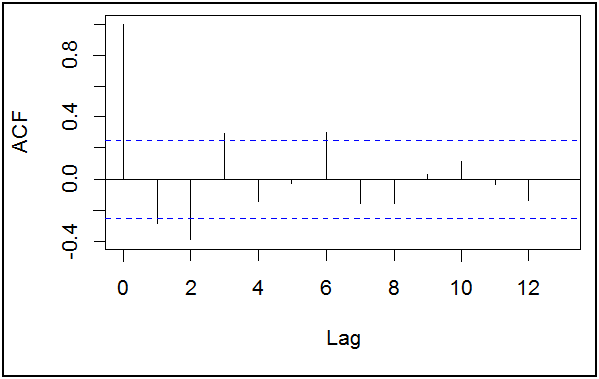
من خلال الشكل أعلاه من خلال الأعمدة التي تلي العمود الأول و التي تكون معنوية (أي خارج مجال الثقة –الخطين المتقطعين-)، و عليه نلاحظ أن الأعمدة 1 و 2 و 3 خارج مجال الثقة، أما بقية الأعمدة من 4 و حتى 13 عموما داخل مجال الثقة.

- تحديد درجة إبطاء AR(p): يكون ذالك من خلال دالة الارتباط الذاتي الجزئي PACF، بالشكل التالي:

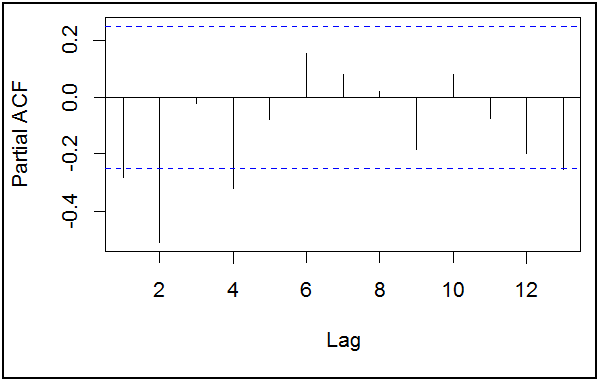
من خلال الشكل أعلاه من خلال الأعمدة التي تكون معنوية (أي خارج مجال الثقة –الخطين المتقطعين-)، و عليه نلاحظ أن الأعمدة 1 و 2 خارج مجال الثقة، أما بقية الأعمدة من 3 و حتى 13 عموما داخل مجال الثقة.

و عليه تكون النماذج التالية هي المرشحة:

ARMA(2,2,0), ARMA(2,2,1), ARMA(2,2,2), ARMA(2,2,3), ARMA(1,2,0), ARMA(1,2,1),ARMA(1,2,2), ARMA(1,2,3), ARMA(0,2,1), ARMA(0,2,2), ARMA(0,2,3).

2- التقدير Estimation:

النماذج 11 المرشحة في مرحلة التعرف يتم تقديرها بالشكل التالي:

مثال نموذج ARMA(2,2,0): نستعمل السلسلة الأصلية (لأننا نحتاجها في التنبؤ بالقيم الحقيقية):

model<-arima(edd,order = c(2,2,0))

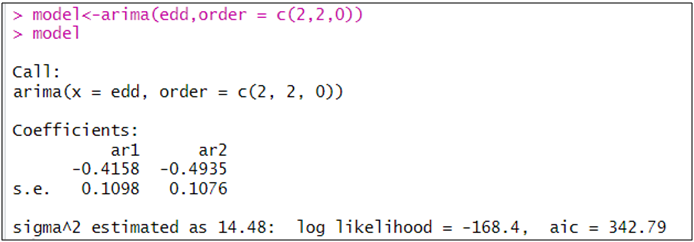
البرنامج قدر نموذج ARMA(2,2,0) بدون ثابت، في حالة تم تقدير النموذج بثابت و أردنا تقدير النموذج بدون ثابت (لربما أنه غير معنوي)نقوم بالأمر:

model<-arima(edd,order = c(2,2,0),include.mean = FALSE)

برنامج R لا يعطينا معنوية المعلمات بطريقة مباشرة، لكن يمكن استخراجها بالأمر:

(1-pnorm(abs(model$coef)/sqrt(diag(model$var.coef))))*2

ملاحظة: نموذج ARMA صالح للتنبؤ فقط و لا يمكن تفسير معلماته كما في الانحدار العادي، ما يمكن رصده من نتائج تقدير نموذج ARMA(2,2,0) هو:

المعلمتين ar1 و ar2 معنويتين حيث الاحتمال أقل من 5 بالمائة.

تدوين إحصائية AIC (Akaike ) لأننا سنختار النماذج من بين 11 نموذج ذي أقل قيمة لهذه الإحصائية، و تساوي 342.79.

مثال نموذج ARMA(2,2,1): نستعمل السلسلة الأصلية:

model2<-arima(edd,order = c(2,2,1))

استخراج معنوية المعلمات:

(1-pnorm(abs(model2$coef)/sqrt(diag(model2$var.coef))))*2

المعلمة ar2 فقط معنوية حيث الاحتمال أقل من 5 بالمائة.

إحصائية AIC (Akaike ) تساوي 344.09.

و هكذا بالنسبة لبقية النماذج 9 المتبقية.

3- التشخيص أو الضبط Diagnostic:

 يجب أن تجتاز هذه النماذج المقدرة المراحل الموالية حتى تكون صالحة للمرحلة الأخيرة و هي التنبؤ:

- معنوية المعلمات.

- خلو البواقي من المشاكل القياسية.

- أدنى إحصائية لمعيار AIC.

نختار مثلا النموذج ARMA(2,2,0) لنطبق عليه هذه الاختبارات:

فيما يخص معنوية المعلمات و إحصائية AIC تم رصدهم في المرحلة السابقة، أما تشخيص البواقي فيكون بتحقق الاختبارات الأساسية التالية حتى يكون النموذج المقدر جيدا:

-عدم وجود ارتباط ذاتي للبواقي  No Autocorrelation:

يمكن اختبار هذه الفرضية فقط باختبار Box–Pierce or Ljung–Box Test Statistic اللذان يدخلان تحت مسمى Portmanteau Tests، و يأخذ الصيغة التالية في البرنامج:

الاختباران يفحصان الفرضيتان:

H0: عدم وجود ارتباط ذاتي

H1: وجود ارتباط ذاتي

Box.test(x, lag = 1, type = c("Box-Pierce", "Ljung-Box"), fitdf = 0)

نستخرج سلسلة البواقي:

residmodel<-model$residuals

Box.test(residmodel, lag = 13, type = c("Box-Pierce", "Ljung-Box"), fitdf = 2)

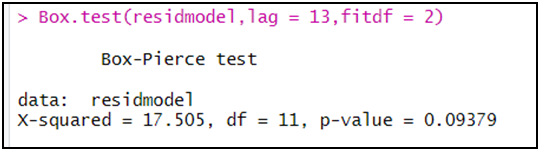
بما أن الاحتمال (p-value) أكبر من 5 بالمائة فإننا لا يمكن أن نرفض الفرضية الصفرية

و القائلة بعدم وجود ارتباط ذاتي لسلسلة البواقي، إذا سلسلة البواقي للنموذج المقدر سحابة بيضاء.

-التوزيع الطبيعي للبواقي  Normality:

يمكن الكشف عن التوزيع الطبيعي بيانيا:

qqnorm(residmodel)

qqline(residmodel)

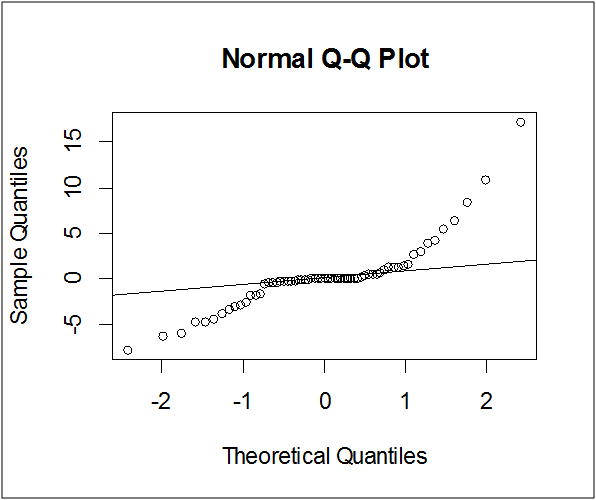
نلاحظ عدم تطابق النقاط مع الخط و بالتالي هناك احتمالية كبيرة أن سلسلة البواقي لا تتبع التوزيع الطبيعي.

هناك اختبارات عدة للتوزيع الطبيعي، و أبرزها Jarque Bera Test:

الاختبار يفحص الفرضيتان:

H0: المتغير يتبع التوزيع الطبيعي

H1: المتغير يتبع لا التوزيع الطبيعي

نستدعي حزمة (tseries):

library(tseries)

jarque.bera.test(residmodel)

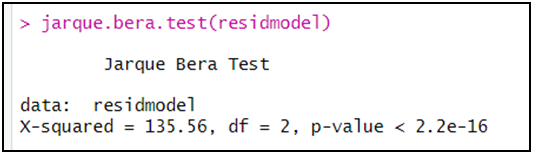
بما أن الاحتمال (p-value) أقل من 5 بالمائة فإننا نرفض الفرضية الصفرية

و نقبل الفرضية البديلة و القائلة بعدم التوزيع الطبيعي لسلسلة البواقي، و بالتالي هذا إخفاق لهذا النموذج.

- ثبات تباين البواقي Homoscedasticity:

يمكن التأكد بيانيا:

plot(residmodel,type="p")

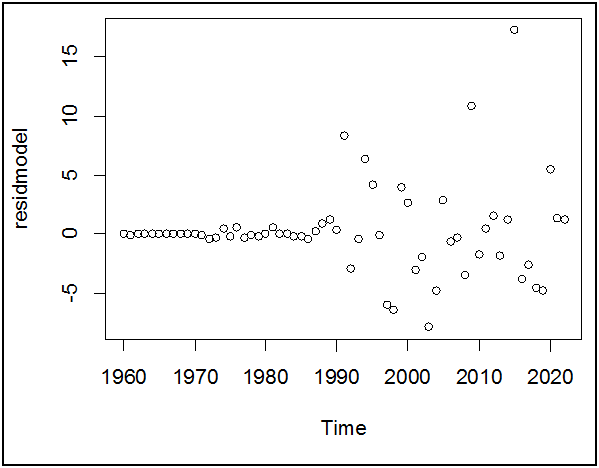
الملاحظ أن هناك مشكلة عدم تجانس التباين Heteroscedasticity، و ذلك لأن البواقي يزيد تشتتها مع الزمن، لكن الاختبار الإحصائي أدق.

هناك اختبارات عدة لتباين البواقي، و منها ARCH Engle's Test:

الاختبار يفحص الفرضيتان:

H0: Homoscedasticity

H1: Heteroscedasticity

نستدعي حزمة (aTSA):

library(aTSA)

arch.test(model)

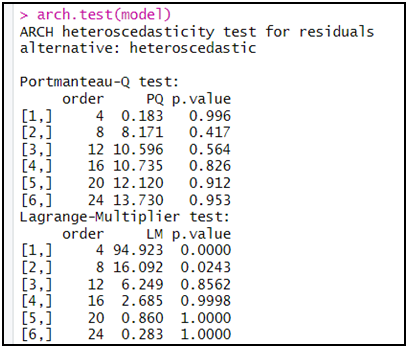
بما أن الاحتمال (p-value) أكبر من 5 بالمائة كلما زادت درجة التأخير
فإننا لا يمكن أن نرفض الفرضية الصفرية و القائلة بتجانس تباين البواقي،
و بالتالي هذا شيء جيد للنموذج

4- التنبؤ Prediction:

بعد اختيار النموذج الذي يتصف:

-معنوية المعلمات.

-خلو البواقي من المشاكل القياسية.

-أدنى إحصائية لمعيار AIC.

يمكن إجراء التنبؤ، لكن لكون نموذج ARMA مقدر بسلسلة مستقرة فإنها لا تحمل معلومات الأجل الطويل، و لهذا لا يجب الإكثار من الفترات المستقبلية للتنبؤ.

نواصل العمل على نموذج ARMA(2,2,0) لنستخدمه للتنبؤ من سنة 2023 إلى 2027:

pred<-predict(model, n.ahead = 5)

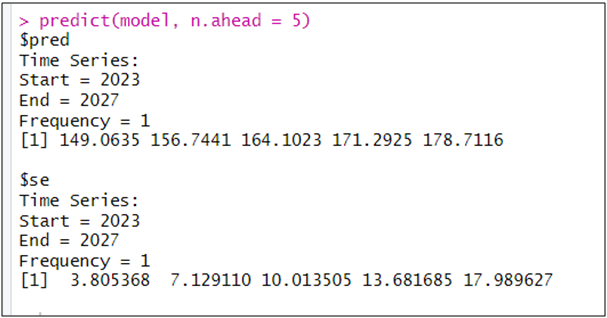
بيانيا:

ts.plot(edd, pred$pred, lty = c(1,3), col=c(1,2))