المحاضرة 08+التطبيق08
1- التعرف أو التحديد Identification:
تعتبر أصعب مرحلة حيث يتم اختيار معين ARIMA(p,I,q)، و يجب أن يجتاز كل المعايير و الاختبارات و إلا نعيد اختيار نموذج أخر أفضل، و تتم العملية كالتالي:
مثال 01: الناتج الداخلي الخام GDP بالدولار الأمريكي بالأسعار الثابتة لسنة 2015 خلال (1960-2022)، طبيعة البيانات سنوية.
رابط المعطيات:
https://data.worldbank.org/indicator/NY.GDP.MKTP.KD?locations=DZ
إنشاء صفحة جديدة في Excel تحتوي فقط: المتغير و السنوات:
نسخ المتغير المدروس:

نختار الأمر collage spécial و نؤشر على transposé
و نفس المراحل بالنسبة لمتغير السنوات:
لنحصل على قاعدة المعطيات التي أسميناه "gdpdz":

نقوم باستيراد قاعدة المعطيات: علما أن الصفحة المقصودة هي feuil1 و أن السنوات طبيعتها رقمية (طريقة الاستيراد تم التطرق لها سابقا):
التعريف بالسلسلة الزمنية:
gdp<-ts(gdpdz$gdp,start=1960)
أ- التمثيل البياني للسلسلة الزمنية:
plot(gdp)
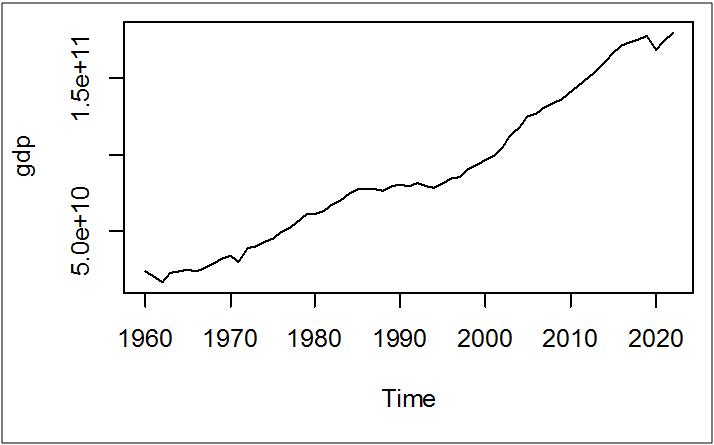
يمكن إدخال اللوغاريتم الطبيعي على السلسلة لتصبح خطية أكثر (شرط عدم وجود قيم سالبة):
lgdp<-log(gdp)
plot(lgdp)
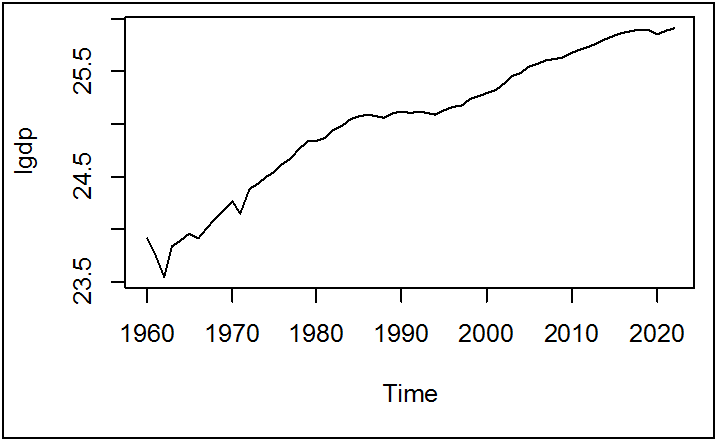
الملاحظ من الشكل البياني ما يلي:
- وجود اتجاه عام تصاعدي: احتمال كبير أن السلسلة غير مستقرة
- عدم وجود نقاط شاذة أو تغيرات هيكلية تؤثر بشكل واضح في نمط السلسلة.
- احتمال كبير أن السلسلة خطية و بالتالي صالحة للنمذجة باستخدام نموذج ARIMA.
ب- دراسة استقرارية السلسلة الزمنية:
بشكل عام اختبارات الاستقرارية مبنية على الفرضيتين:
H0: عدم الاستقرارية (Nonstationarity)
H1: وجود استقرارية (stationarity)
نحتاج حزمة (tseries):
library(tseries)
adf.test(lgdp)

الملاحظ أن اختبار ADF بين أن السلسلة lgdp غير مستقرة، و ذلك من خلال عدم رفض الفرضية الصفرية و ذلك كون أن الاحتمال (p-value) أكبر من 5 بالمائة.
يمكن التأكد باستخدام اختبار ثاني:
pp.test(lgdp)
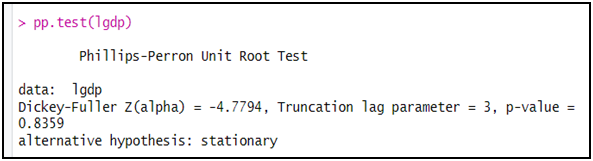
الملاحظ أن اختبار PP بين كذلك أن السلسلة lgdp غير مستقرة، و ذلك من خلال عدم رفض الفرضية الصفرية و ذلك كون أن الاحتمال (p-value) أكبر من 5 بالمائة.
خلاصة:بينت الاختبارات أن السلسلة lgdp غير مستقرة، و عليه يجب جعلها مستقرة حتى يمكن نمذجتها باستخدام نموذج ARIMA.
يمكن أن نعمل لها الفروق من الدرجة الأولى (يرى الباحثون المختصون في السلاسل الزمنية أن أغلبية المتغيرات الاقتصادية هي من نوع DS و بالتالي يمكن أن تستقر بإجراء الفروق) و نعيد اختبارات الاستقرارية:
dlgdp<-diff(lgdp,differences = 1)
الرقم 1 يعني الفروق من الدرجة الأولى، و 2 يعني الفروق من الدرجة الثانية،...إلخ.
plot(dlgdp)
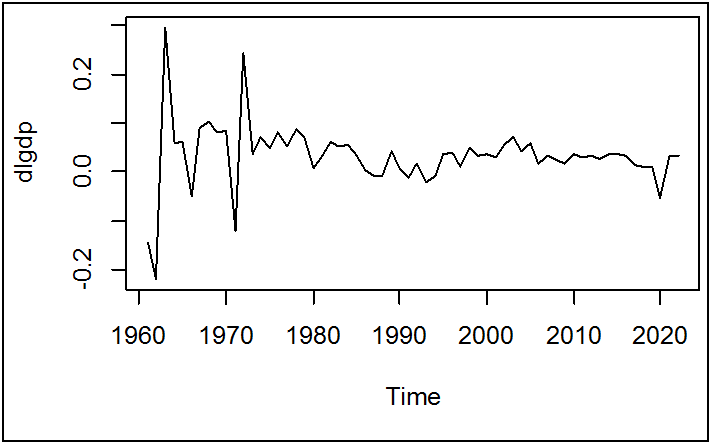
الملاحظ أن سلسلة الفروق يمكن أن تكون مستقرة.
adf.test(dlgdp)

الملاحظ أن اختبار ADF بين أن السلسلة dlgdp مستقرة، و ذلك من خلال رفض الفرضية الصفرية و ذلك كون أن الاحتمال (p-value) أقل من 5 بالمائة.
يمكن التأكد باستخدام اختبار ثاني:
pp.test(dlgdp)
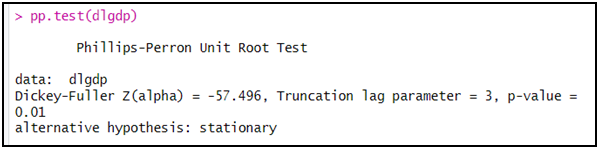
الملاحظ أن اختبار PP بين كذلك أن السلسلة lgdp مستقرة، و ذلك من خلال رفض الفرضية الصفرية و ذلك كون أن الاحتمال (p-value) أقل من 5 بالمائة.
خلاصة:بينت الاختبارات أن السلسلة lgdp مستقرة، و بالتالي يمكن نمذجتها باستخدام نموذج ARIMA، و بما أن السلسلة المدروسة تطلبت الفرق الأول فقط لتستقر فإن النموذج يكون من الشكل ARIMA(p,1,q).
ج- التأكد من أن السلسلة المستقرة ليست سحابة بيضاء:
ذكرنا سابقا أن كل سحابة بيضاء هي سلسلة مستقرة بينما ليس كل سلسلة مستقرة هي سحابة بيضاء، نلاحظ من الشكل السابق للسلسلة dlgdp ذات المتوسط المقارب للصفر أنه يمكن أن تكون السلسلة الأخيرة سحابة بيضاء، يمكن التأكد باستعمال اختبار Box–Pierce or Ljung–Box Test Statistic، حيث الاختباران يفحصان الفرضيتان:
H0: عدم وجود ارتباط ذاتي
H1: وجود ارتباط ذاتي
بما أن حجم العينة هو 61 مشاهدة (لأنها سلسلة فروق طرحت منها مشاهدة واحدة) سنختار حسب قاعدة Rob J Hyndman درجة التأخير lag المثلى هي 13.
Box.test(dlgdp,lag=13)

بما أن الاحتمال (p-value) أكبر من 5 بالمائة فإنه لا يمكننا رفض الفرضية الصفرية
.و القائلة بعدم وجود ارتباط ذاتي للسلسلة المدروسة، إذا السلسلة الزمنية dlgdp سحابة بيضاء
الخلاصة السلسلة dlgdp سلسلة مستقرة لكن لا يمكن نمذجتها لأنها سحابة بيضاء.
