المحاضرة 07+التطبيق07

الشكل الرياضي لنموذج ARIMA:

مراحل نموذج ARIMA:

لنموذج ARIMA مراحل أربعة معروفة:

1- التعرف أو التحديد Identification

2- التقدير Estimation

3- التشخيص أو الضبط Diagnostic

4- التنبؤ Prediction

لكن لضمان رصانة الدراسة، يجب أن تسبق هذه المراحل الكشف عن تحقق ما يلي في السلسلة الزمنية:

1- الكشف عن النقاط الشاذة

2- الكشف عن خطية السلسلة الزمنية

3- الكشف عن التغيرات الهيكلية:

4- اختبار الاتجاه العام في السلسلة

و عدم الالتزام بهذه الاختبارات يؤدي إلى نتائج منها:

-          الحصول على علاقة غير حقيقية.

-          القيام(عدم القيام) باختبارات لم يكن من الضروري (كان من الواجب) القيام بها.

-          معاناة النموذج من مشاكل في البواقي.

1- الكشف عن النقاط الشاذة:

نماذج ARIMA تتأثر بالقيم الشاذة، فإن كانت مبررة اقتصاديا (أزمة اقتصادية أو تطبيق سياسة معينة) ندخلها في النموذج (من بين النماذج المستخدمة هو Robust ARIMA) أما إن كانت مجرد أخطاء قياس فيجب تصحيحها.

كما رأينا سابقا يمكن الكشف عن النقاط الشاذة عن طريق "شكل الصندوق" (boxplot): حيث النقاط خارج الصندوق هي المشاهدات الشاذة.

و عليه سنحتاج تثبيت الحزمة (outliers).

بشكل عام اختبارات النقاط الشاذة مبنية على الفرضيتين:

H0: المشاهدة ليست نقطة شاذة

H1: المشاهدة نقطة شاذة

مثال 01: إنشاء سلسلة عشوائية بمقاطع مختلفة تتبع التوزيع الطبيعي:

y<-c(rnorm(50,9,1.5),rnorm(50,8,1),rnorm(100,7,1))

plot(y,type="l")

مثلا يمكن رصد بيانيا النقاط الشاذة في الدوائر الحمراء.

library(outliers)

chisq.out.test(y)

grubbs.test(y)

الملاحظ أن الاختبارين اتفقا على أن المشاهدة التي قيمتها 12.28 في السلسلة y تعتبر نقطة شاذة، و ذلك من خلال رفض الفرضية الصفرية و ذلك كون أن الاحتمال (p-value) أقل من 5 بالمائة.

ملاحظة:هذه الاختبارات تكشف عن نقطة شاذة واحدة فقط و عليه يجب تكرار الاختبار للكشف عن بقية النقاط الشاذة.

إضافة: يمكن كتابة الأوامر السابقة بالشكل:

chisq.out.test(y,type=11)

10: أكبر قيمة عن المتوسط هي نقطة شاذة (by default)

11:  أكبر و أصغر قيمتين عن المتوسط هما نقطتان شاذتان

معالجة النقاط الشاذة إذا كانت بسبب أخطاء قياس:

و عليه سنحتاج تثبيت الحزمة (timetk).

مثال: لدينا السلسلة التالية:

a<-(2,3,4,5,6,8,7,55,-20)

نضع الأمر التالي للسلسلة المدروسة:

x<-c(rnorm(50,1,1),rnorm(50,2,1),rnorm(50,-10,1))

plot(x,type="l")

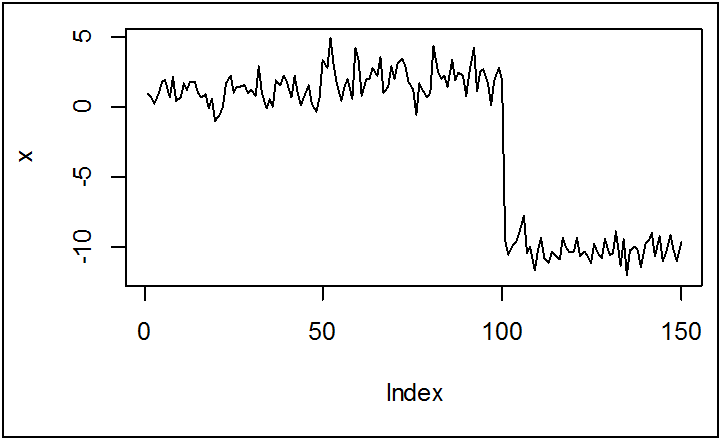
الملاحظ أن السلسلة x غير  خطية من خلال جزئها الثالث بالمقارنة بالجزأين الأولين.

التأكد بالاختبارات:

library(nonlinearTseries)

nonlinearityTest(x)

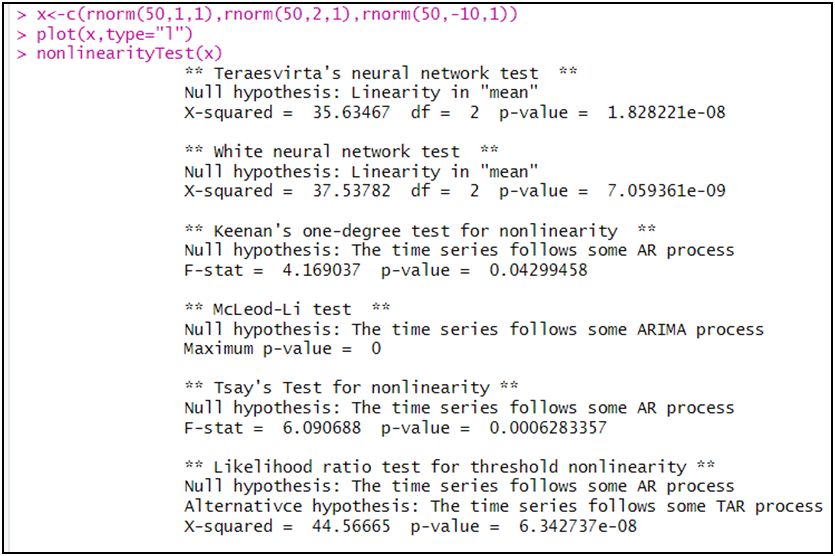
الملاحظ أن الاختبارات الستة اتفقت على عدم خطية السلسلة x، و ذلك من خلال رفض الفرضية الصفرية و ذلك كون أن الاحتمال (p-value) أقل من 5 بالمائة.

ملاحظة: يمكن إذا كانت السلسلة تتبع العلاقة الأسية جعلها خطية بإدخال اللوغاريتم الطبيعي.

النتيجة: يجب نمذجة السلسلة الزمنية x بغير نموذج ARIMA.

مثال 02: إنشاء سلسلة عشوائية بمقاطع مختلفة تتبع التوزيع الطبيعي:

y<-c(rnorm(50,9,1.5),rnorm(50,8,1),rnorm(100,7,1))

plot(y,type="l")

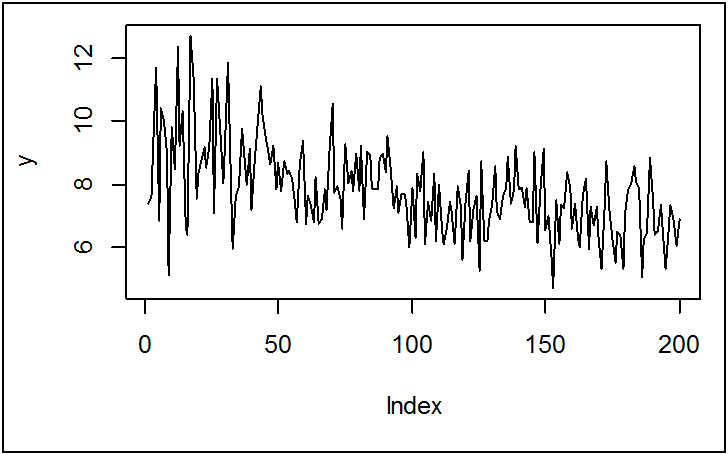
الملاحظ أن السلسلة y خطية.

التأكد بالاختبارات:

nonlinearityTest(y)

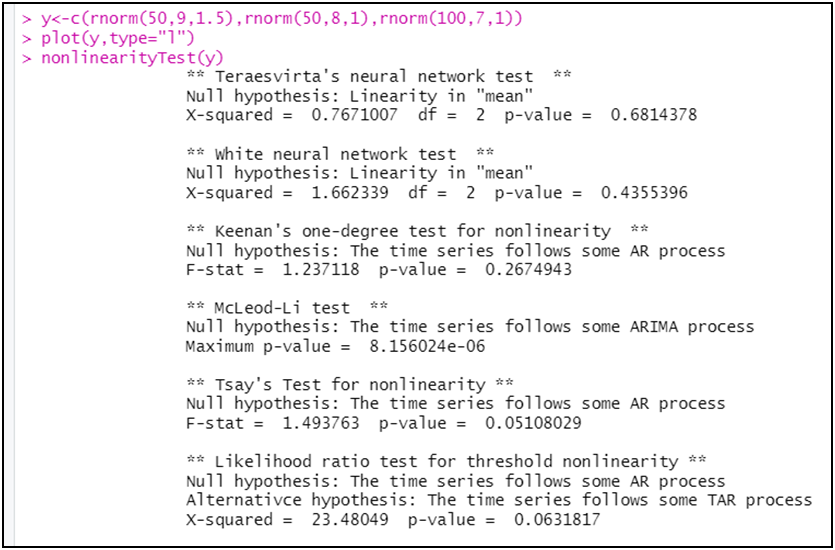
الملاحظ خمسة اختبارات من أصل ستة اتفقت على خطية السلسلة y (يعني الأغلبية، بالإضافة إلى دعم التمثيل البياني لفكرة الخطية)، و ذلك من خلال عدم رفض الفرضية الصفرية و ذلك كون أن الاحتمال (p-value) أكبر من 5 بالمائة.

النتيجة: يمكن نمذجة السلسلة الزمنية y بنموذج ARIMA.

3- الكشف عن التغيرات الهيكلية:

التغير الهيكلي (Structurel Break - SB -) هو عبارة عن حدث (أزمة اقتصادية-حرب-قرار اقتصادي...) يؤدي إلى تغير نمط السلسلة الزمنية، حيث يمكن أن يغير في متوسطها (المشاهدة 101 للمثال 01 في الكشف عن الخطية) أو تباينها أو اتجاهها.

قوة اختبارات جذر الوحدة العادية مثل: KPSS-PP-ADF و غيرها ضعيفة في حالة وجود SB، حيث أن SB تديم الصدمات و يظهر لنا أن هناك جذر الوحدة، لكن الحقيقة عكس ذلك، أي نتيجة هذه الاختبارات العادية تكون خاطئة، و عليه القيام بالفروق لتستقر السلسلة يكون كذلك قرار خاطئ، و هناك اختبارات الاستقرارية للكشف عن التغيرات الهيكلية، و تتنوع من حيث:

- التغير الهيكلي المؤثر في متوسط السلسلة أو اتجاهها العام أو معا.

- التغير الهيكلي المفاجئ أو بالتدرج.

- التغير الهيكلي الخارجي (يحدد الباحث) أو الداخلي (يحدده الاختبار)

- التغير الهيكلي الوحيد أو المتعدد.

و من بين هذه الاختبارات نجد:

4- اختبار الاتجاه العام في السلسلة:

إن وجود الاتجاه العام أو الثابت في السلسلة الزمنية أو عدم وجودهما له تأثير على نتائج اختبار جذر الوحدة، و بالتالي استقرارية أو عدم استقرارية السلسلة الزمنية، و إن كان تحديد وجود الثابت يمكن معرفته من كون السلسلة تنطلق من الصفر (عدم وجود ثابت) أو لا تنطلق من الصفر (وجود ثابت)، فإن الاتجاه العام أحيانا يكن واضح من أن السلسلة الزمنية أنها تحتوي اتجاه عام (تصاعدي أو تنازلي) لكن أحيانا أخرى تكون الملاحظة الشكلية أقل وضوح و لهذا نلجأ إلى اختبارات الاتجاه العام و منها اختبار "مان-كيندال" (Mann-Kendall Trend Test).

سنحتاج تثبيت الحزمة (trend).

بشكل عام اختبارات الاتجاه العام مبنية على الفرضيتين:

H0: لا يوجد اتجاه عام في السلسلة

H1: يوجد اتجاه عام في السلسلة

مثال 01: إنشاء سلسلة عشوائية بمقاطع متفاوته لتبيان عدم وجود اتجاه عام.

x<-c(rnorm(50,7,1),rnorm(40,3,0.8),rnorm(60,10,1),rnorm(50,3,1.1),rnorm(20,8,1.2))

plot(x,type = "l")

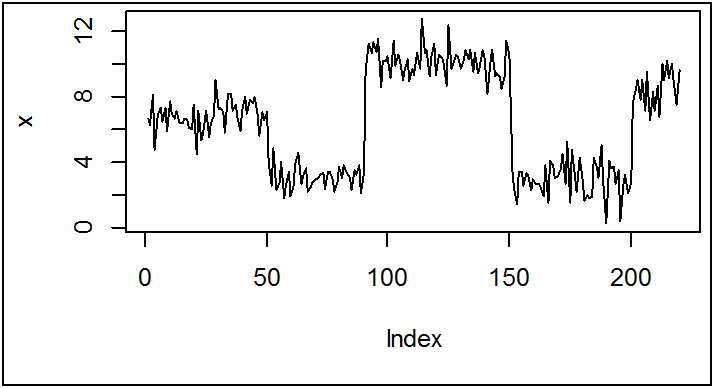
الملاحظ أن السلسلة x لا تحتوي اتجاه عام فمرة في صعود و مرة في هبوط، يعني ليس لها منحى واحد تتبعه.

التأكد بالاختبارات:

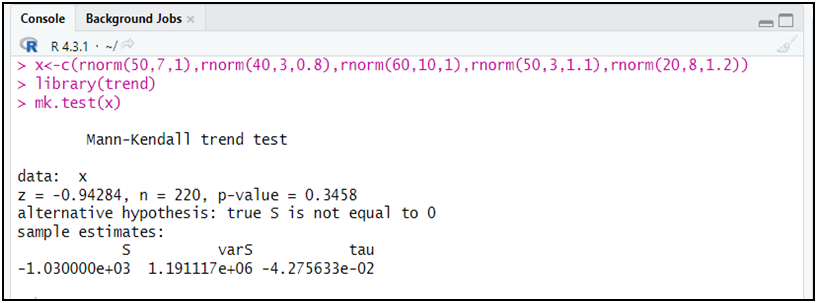
الملاحظ أن الاختبار أقر بعدم وجود اتجاه عام في السلسلة x، و ذلك من خلال عدم رفض الفرضية الصفرية و ذلك كون أن الاحتمال (p-value) أكبر من 5 بالمائة.

النتيجة: السلسلة الزمنية x تحتوي ثابت فقط لأن أول قيمة غير معدومة (6.68) و لا تحتوي اتجاه عام:(Intercept).

مثال 02: إنشاء سلسلة عشوائية بمقاطع متفاوته لتبيان وجود اتجاه عام.

y<-c(rnorm(50,2,1),rnorm(40,3,0.8),rnorm(60,5,1),rnorm(10,3.5,1.1),rnorm(20,6,1.2))

plot(y,type = "l")

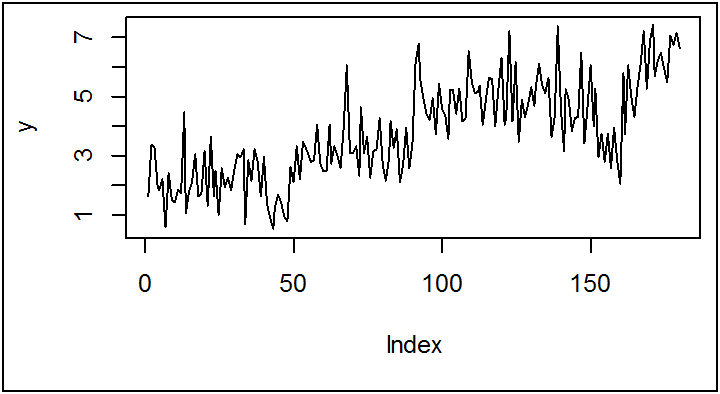
الملاحظ أن السلسلة y تحتوي اتجاه عام تصاعدي.

التأكد بالاختبارات:

mk.test(y)

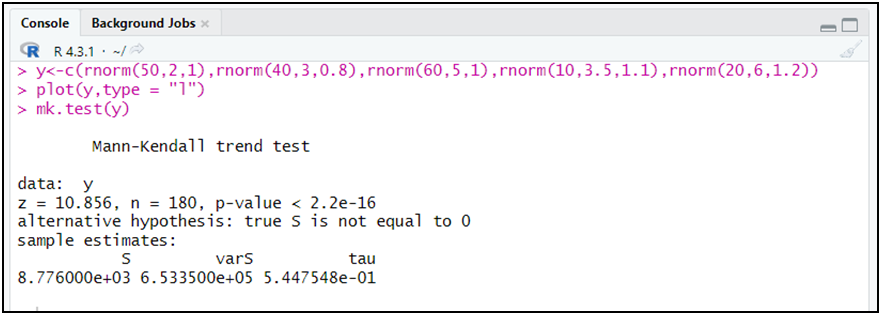
الملاحظ أن الاختبار أقر بوجود اتجاه عام في السلسلة y، و ذلك من خلال رفض الفرضية الصفرية و ذلك كون أن الاحتمال (p-value) أقل من 5 بالمائة.

النتيجة: السلسلة الزمنية y تحتوي ثابت لأن أول قيمة غير معدومة (1.63) و تحتوي اتجاه عام: (Trend+Intercept).