المحاضرة 06+التطبيق06
مقدمة عن السلاسل الزمنية:
لبرنامج R عديد الأوامر و الحزم للتعامل مع السلاسل الزمنية بكل سهولة.
-التعريف بالسلسلة الزمنية: مثلا سلسلة زمنية سنوية x تبدأ سنة 1990:
x<-ts(x,start=1990)
في حالة كانت السلسلة نصف سنوية:
x<-ts(x,start=1990, frequency =2)
الأمر |
العدد |
التردد |
frequency=360 |
360 |
يومي |
|
frequency = 52 |
52 |
أسبوعي |
|
frequency = 12 |
12 |
شهري |
|
frequency = 4 |
4 |
ثلاثي |
|
frequency = 2 |
2 |
سداسي |
|
frequency = 1 , by default |
1 |
سنوي |
ملاحظة: أي نضع الرقم في التردد بعدد ظهور المشاهدة خلال سنة واحدة.
2- دالة الارتباط الذاتي للكشف عن السحابة (ضجة) البيضاء:
شروط كون السلسلة سحابة بيضاء ثلاثة هي:
1- المتوسط يساوي "0".
2- التباين ثابت .
3- التباين المشترك يساوي "0".
أ- الكشف عن السحابة البيضاء بيانيا:
- مثال عن سلسلة صالحة للنمذجة:
التمثيل البياني للسلسلة:
plot(x)
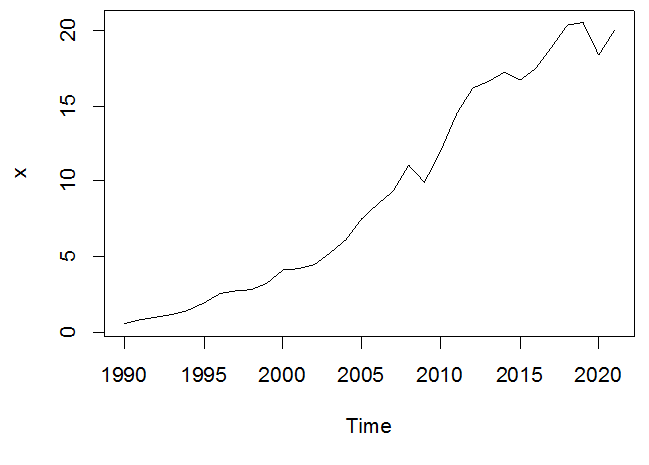
الملاحظ على السلسلة وجود اتجاه عام تصاعدي و بالتالي هناك احتمال جد كبير على أن السلسلة ليست سحابة بيضاء.
acf(x)
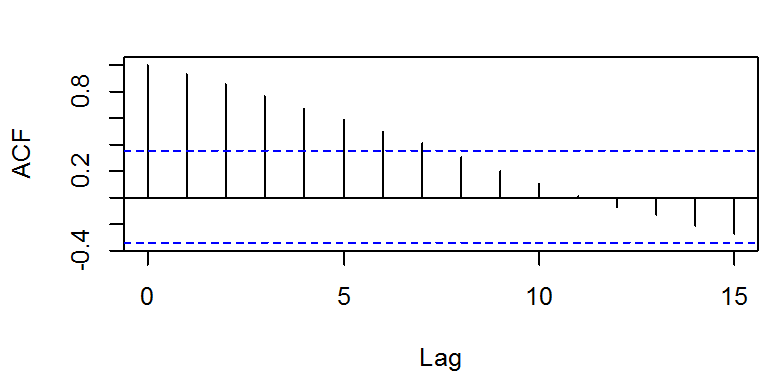
الملاحظ أن الرسم أعلاه (مخطط الارتباط Correlogram) ليس سحابة بيضاء و ذلك لأن هناك خطوط خارج مجال الثقة و بالتالي هذه السلسلة صالحة النمذجة.
- مثال عن سلسلة غير قابلة للنمذجة (سحابة بيضاء):
التمثيل البياني للسلسلة:
plot(y)
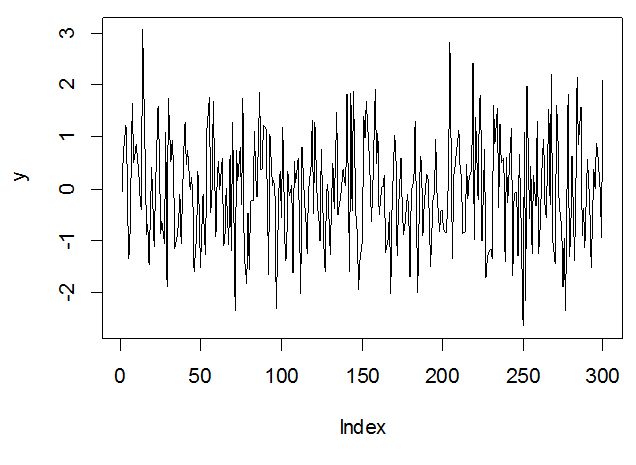
الملاحظ على السلسلة على أنها تملك متوسط معدوم و تباين ثابت، و بالتالي احتمال أن تكون سحابة بيضاء.
acf(y)

الملاحظ أن الرسم أعلاه (مخطط الارتباط Correlogram) سحابة بيضاء و ذلك لأن كل الخطوط داخل مجال الثقة و بالتالي هذه السلسلة غير صالحة للنمذجة.
ملاحظة: الخط الأول دائما خارج مجال الثقة، و عليه لا يعتد به.
ب- السحابة البيضاء إحصائيا:
و ذلك باستخدام اختبار Box–Pierce or Ljung–Box Test Statistic اللذان يدخلان تحت مسمى Portmanteau Tests، و يأخذ الصيغة التالية في البرنامج:
الاختباران يفحصان الفرضيتان:
H0: عدم وجود ارتباط ذاتي
H1: وجود ارتباط ذاتي
Box.test(x,lag=1,type=c("Box-Pierce","Ljung-Box"),fitdf=0)
lag : حسب الخبير في السلاسل الزمنية Rob J Hyndman فإن درجة التأخير lag المثلى تكون
من المشاهدة الأولى إلى حجم العينة مقسمة على الرقم 5.fitdf: هذا الأمر خاص بسلاسل البواقي.
Box.test(x,lag = 6)
Box-Pierce test
data: x
X-squared = 102.79, df = 6, p-value < 2.2e-16
بما أن الاحتمال (p-value) أقل من 5 بالمائة فإننا نرفض الفرضية الصفرية و نقبل الفرضية البديلة
و القائلة بوجود ارتباط ذاتي للسلسلة المدروسة، إذا السلسلة الزمنية x ليست سحابة بيضاء.
Box.test(y,lag = 60)
Box-Pierce test
data: y
X-squared = 51.52, df = 60, p-value = 0.7741
بما أن الاحتمال (p-value) أكبر من 5 بالمائة فإنه لا يمكن رفض الفرضية الصفرية و القائلة
بعدم وجود ارتباط ذاتي للسلسلة المدروسة، إذا السلسلة الزمنية y سحابة بيضاء، لا نستطيع نمذجتها.
خلاصة: الاختبار الإحصائي وافق الملاحظات المستقاة من الرسم البياني.
3- استقرارية السلاسل الزمنية:
علاقة الاستقرارية بالسحابة البيضاء:
- كل سلسلة سحابة بيضاء هي مستقرة.
- ليس كل سلسلة مستقرة هي سحابة بيضاء.
شروط كون السلسلة مستقرة ثلاثة هي:
1- المتوسط ثابت عبر الزمن.
2- التباين ثابت عبر الزمن.
3- التباين المشترك ثابت عبر الزمن.
أشكال سلاسل غير مستقرة:
المتوسط غير ثابت و التباين ثابت
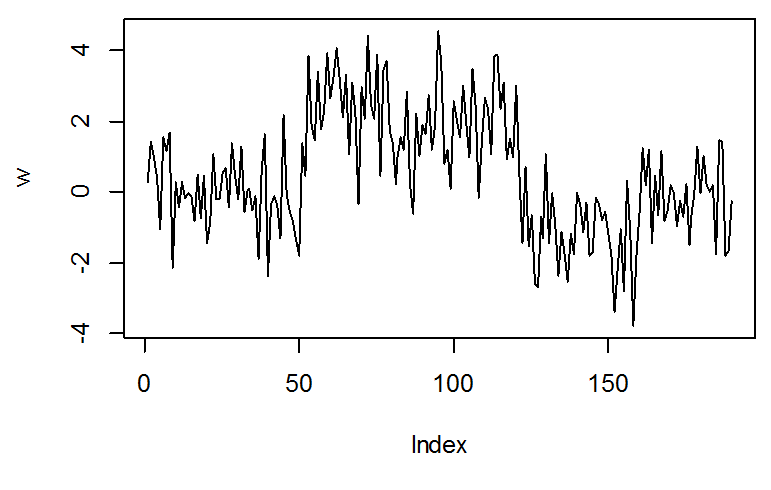
المتوسط ثابت و التباين غير ثابت
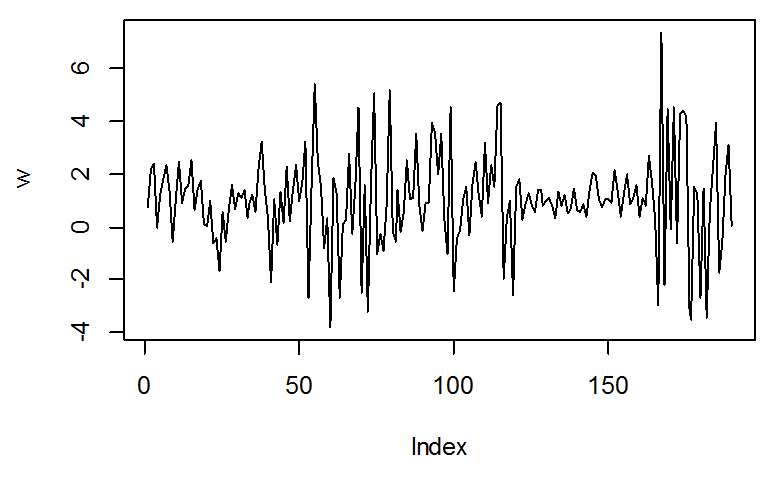
المتوسط غير ثابت و التباين غير ثابت

سلسلة غير مستقرة تحتوي الموسمية
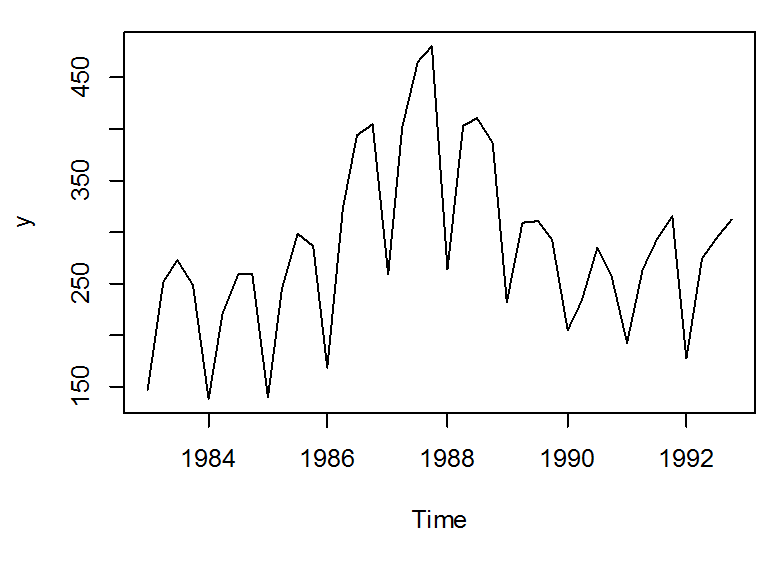
سلسلة غير مستقرة تحتوي اتجاه عام صاعد
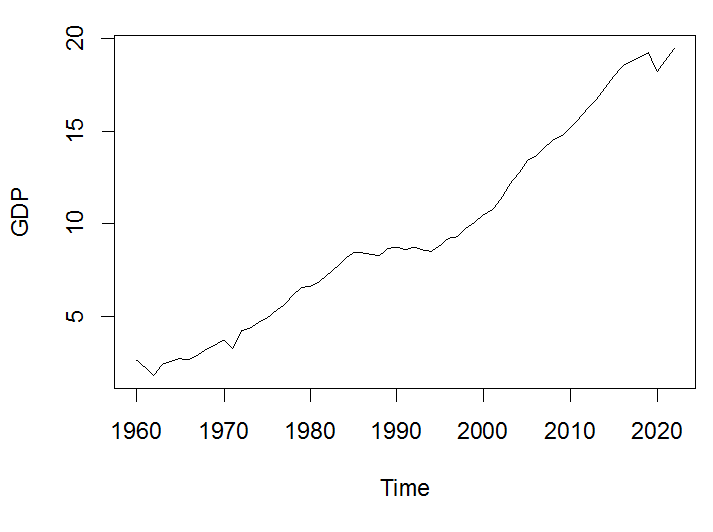
سلسلة غير مستقرة تحتوي اتجاه عام تنازلي
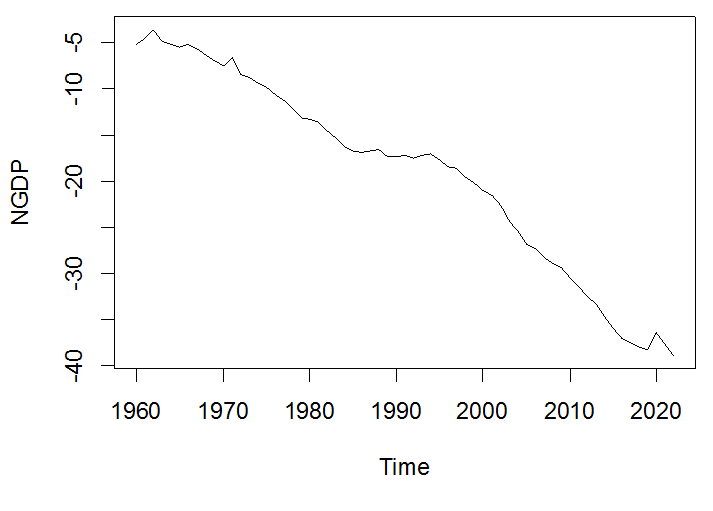
الكشف عن الاستقرارية باستخدام الاختبارات:
اختبارات الاستقرارية عديدة أبرزها:
adf.test (Augmented Dickey–Fuller Test -1993-)
pp.test (Phillips–Perron Unit Root Test - 1993 -)
kpss.test (Kwiatkowski-Phillips-Schmidt-Shin - 1992 -)
بشكل عام اختبارات الاستقرارية مبنية على الفرضيتين:
H0: عدم الاستقرارية (Nonstationarity)
H1: وجود استقرارية (stationarity)
نحتاج حزمة (tseries):
library(tseries)
مثال: انشاء سلسلة عشوائية غير مستقرة
x<-c(rnorm(25,3,2),rnorm(30,5,1.8),rnorm(40,6.5,1.5),rnorm(55,14,1.4))
plot(x,type="l")
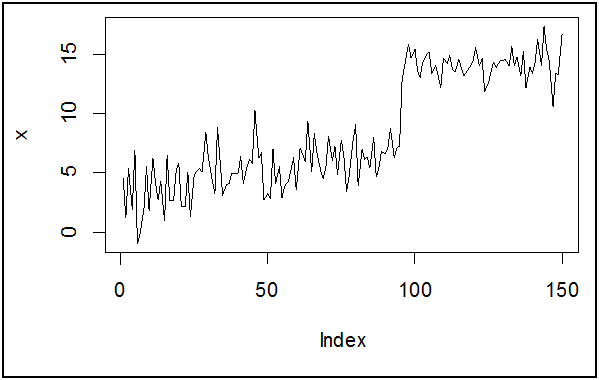
الملاحظ على السلسلة أنها تملك اتجاه عام تصاعدي و بالتالي من المحتمل جدا أنها غير مستقرة.
adf.test(x)
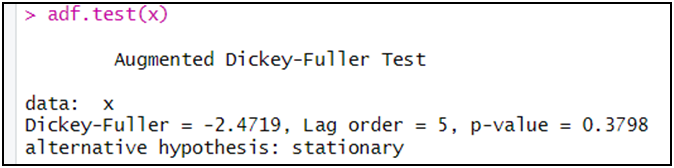
الملاحظ أن اختبار ADF بين أن السلسلة x غير مستقرة، و ذلك من خلال عدم رفض الفرضية الصفرية و ذلك كون أن الاحتمال (p-value) أكبر من 5 بالمائة (37.98 بالمائة).
يمكن التأكد باستخدام اختبار ثاني:
pp.test(x)
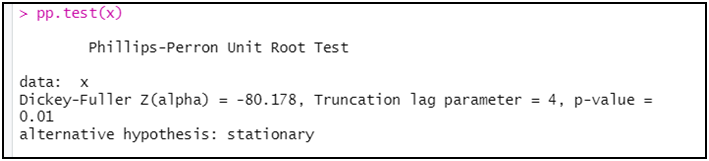
الملاحظ أن اختبار pp بين أن السلسلة x مستقرة، و ذلك من خلال رفض الفرضية الصفرية و قبول الفرضية البديلة و القائلة باستقرار السلسلة الزمنية و ذلك كون أن الاحتمال (p-value) أقل من 5 بالمائة (1 بالمائة).
يمكن الاستعانة باختبار KPSS للفصل في هذا التناقض بين ADF و PP، و اختبار KPSS مبني على الفرضيتين التاليتين (عكس بقية اختبارات جذر الوحدة):
H0: وجود استقرارية (stationarity)
H1: عدم الاستقرارية (Nonstationarity)
kpss.test(x)

الملاحظ أن اختبار KPSS بين أن السلسلة x غير مستقرة، و ذلك من خلال رفض الفرضية الصفرية و قبول الفرضية البديلة و القائلة بعدم استقرار السلسلة الزمنية و ذلك كون أن الاحتمال (p-value) أقل من 5 بالمائة (1 بالمائة).
خلاصة: السلسلة x مستقرة يمكن نمذجتها باستخدام نموذج ARIMA
ملاحظة: يمكن استخدام حزمة (urca) حيث أنها توفر عدة بدائل لإجراء الاختبارات أعلاه.
