المحاضرة 05+التطبيق 05
1- الإحصاءات الوصفية للمتغيرات المتصلة:
نستدعى قاعدة بيانات البرنامج "mtcars":
View(mtcars)
استخدام دالة (summary) التي تعطينا بعض الإحصاءات:
summary(mtcars)
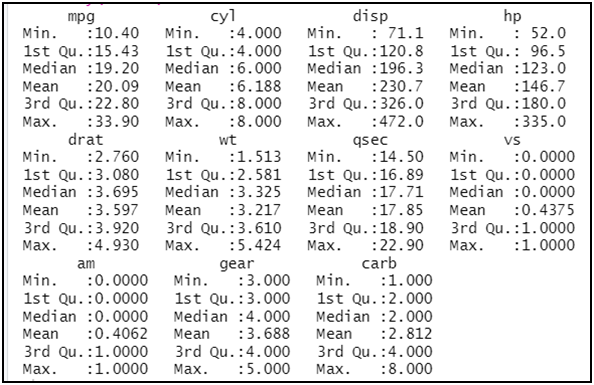
|
min |
أدنى قيمة للمتغير |
1st Qu |
القيمة الواقعة في أعلى الربع الأول بعد ترتيب القيم تصاعديا |
Median |
الوسيط |
Mean |
المتوسط |
3rd Qu |
القيمة الواقعة في أعلى الربع الثالث بعد ترتيب القيم تصاعديا |
Max |
أكبر قيمة للمتغير |
و الدالة السابقة صالحة للمتغيرات المتصلة، و عليه يمكن حصرها لهذه المتغيرات فقط، (نختار المتغيرات الكمية المتصلة فقط (mpg-disp-hp-drat-wt-qsec) بموقعها):
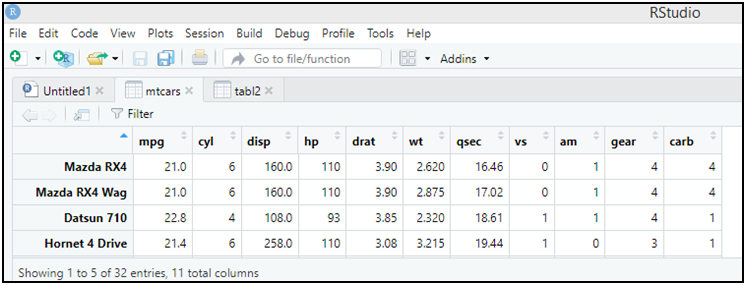
summary(mtcars[,c(1,3:7)])
الأمر الأخير مفاده استخراج إحصائيات للأعمدة (لأن المتغيرات ممثلة بالأعمدة): 1 و من 3 إلى 7. (لم نختر عدد الأسطر لأنه تهمنا كل أنواع السيارات).
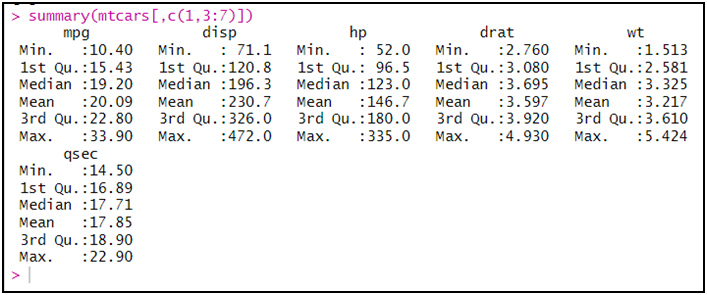
يمكن استخراج إحصاءات أخرى، لكن هي صالحة لكل متغير، منها:
|
sd |
الانحراف المعياري |
|
var |
التباين |
|
sum |
المجموع |
|
range |
المدى و هو الفرق ما بين أعلى قيمة و أدنى قيمة للمتغير |
|
Length |
حجم المشاهدات |
يمكن استخراج إحصاءات أخرى، لكن هي صالحة لعدة متغيرات، منها:
|
cor |
مصفوفة الارتباط |
|
Var أو cov |
مصفوفة التباين و التباين المشترك |


دالة apply: استخراج إحصاءات لعدة متغيرات، حساب المتوسط لكل الأعمدة (المتغيرات):
- للدلالة على الأعمدة (المتغيرات) نضع الرقم 2
- للدلالة على الأسطر (الأفراد) نضع الرقم 1
apply(mtcars,2,mean)

استخراج إحصائية لبعض المتغيرات فقط (لأن بعض الإحصاءات تصلح فقط للمتغيرات المتصلة)، نختار المتغيرات الكمية المتصلة فقط (mpg-disp-hp-drat-wt-qsec) بموقعها:
apply(mtcars[,c(1,3:7)],2,mean)
إنشاء دالة:مثال كل متغير متوسطه مقسم على الانحراف المعياري له:
apply(mtcars[,c(1,3:7)],2,function(x)mean(x)/sd(x))

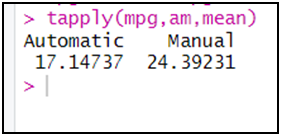
إيجاد إحصائية معينة لمتغير على حسب متغير أخر، شريطة أن يكون الأخير فئوي، مثال: متوسط سنوات الخبرة أو متوسط الأجر الشهري أو ... حسب متغير الجنس.
فيما يلي سنحسب المتوسط من قاعدة بيانات "mtcars" لمتغير: استهلاك الوقود لكل ميل بالجالون لكل نوع من عدد اسطوانات المحرك:
aggregate(mpg~cyl,data= mtcars,mean)
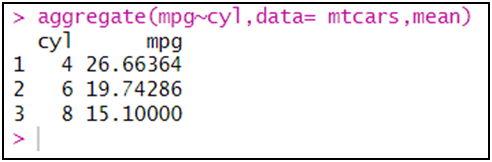
إيجاد إحصائية معينة لمتغيرات على حسب متغير شريطة أن يكون الأخير فئوي:
فيما يلي سنحسب المتوسط من قاعدة بيانات "mtcars" لمتغيري: عدد الأحصنة البخارية و استهلاك الوقود لكل ميل بالجالون لكل نوع من عدد اسطوانات المحرك:
aggregate(cbind(hp,mpg)~cyl,data= mtcars,mean)
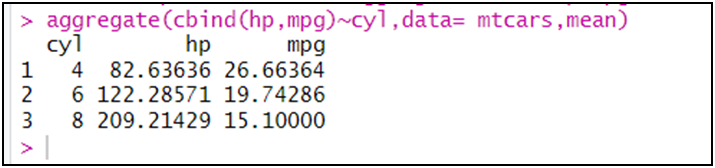
أو إيجاد إحصائية معينة لمتغيرات على حسب عدة متغيرات فئوية:
aggregate(cbind(hp,mpg)~cyl+gear,data= mtcars,mean)
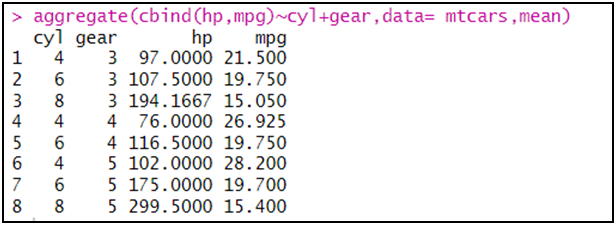
2- الإحصاءات الوصفية للمتغيرات الفئوية:
مثلا نبحث عن متوسط استهلاك الوقود لكل ميل بالجالون لكل نوع من علبة السرعة:
يجب أولا دائما التعريف بأن المتغير فئوي، مثلا متغير نوع علبة السرعة:
أتوماتيكي أو يدوي، لكي لا يعتبرها البرنامج متصلة و يجري عليها بعض العمليات، و
كذلك حتى تظهر أسماء أنواع المتغير، ففي حالتنا:
am<-factor(am,levels = c(0,1),labels = c("Automatic","Manual"))
إنشاء جداول التكرارات و النسب المئوية للمتغيرات الفئوية فيما بينها:
- التكرارات:
مثال: متغير علبة السرعة و متغير عدد اسطوانات المحرك، و لنعرف الأخير على أنه فئوي كما عرفنا الأول سابقا:cyl<-factor(cyl,levels = c(4,6,8),labels = c("4 cylinder","6 cylinder","8 cylinder"))
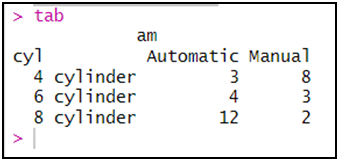
tab<-table(cyl,am)
المتغير المذكور أولا يظهر في الأسطر و الثاني يظهر في الأعمدة.
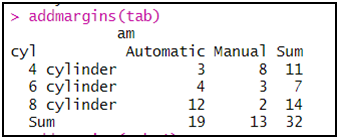
إضافة المجموع عن طريق دالة addmargins للجدول السابق:addmargins(tab)
إضافة المجموع كسطر (أي مجموع كل عمود):addmargins(tab,1)إضافة المجموع كسطر (أي مجموع كل عمود):addmargins(tab,2)
- النسب المئوية:النسب بالنسبة لكل سطرprop.table(tab,1)النسب بالنسبة لكل عمودprop.table(tab,2)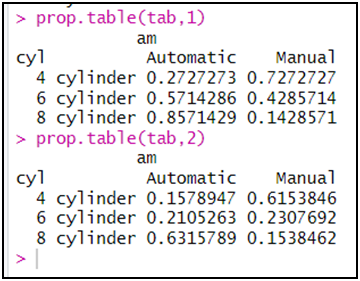
النسب المئوية مع تقريب إلى رقمين بعد الفاصلة (يعني أربعة أرقام ككل)
round(prop.table(tab,2),4)*100
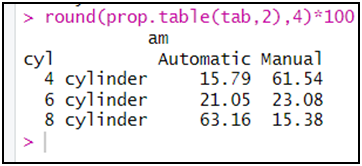
علما أن دالة round في العادة تتعامل مع الأرقام بعد الفاصلة.
مثال: نريد تقريب القيمتين إلى رقمين بعد الفاصلة:
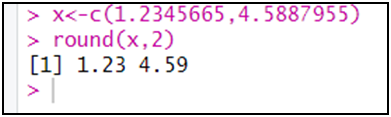
3- حزمة مهمة لعمل الإحصاءات:
حزمة (psych):
بعض الإحصاءات الإضافية مثل
الالتواء و التفرطح: في الأمر 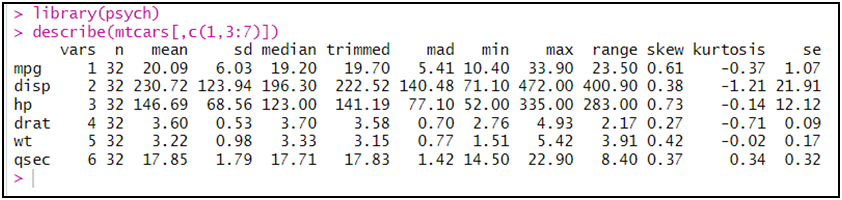
حيث تفيدنا إحصائيتي التفرطح (kurtosis) في معرفة تمركز البيانات و الالتواء (skewness) في معرفة التوزيع الطبيعي للبيانات:
التفرطح: يساوي 3 معتدل، أقل من 3 مفرطح للقمة، أكبر من 3 مدبب للقمة.
الالتواء: حيث إن كانت القيمة ما بين 0.5- و 0.5 يكون التوزيع معتدل، و إن كان خارج 1- و 1 يكون غير معتدل.
trimmed: هو المتوسط الذي لا يأخذ في الحسبان القيم الشاذة، مثلا بعد أن يرتب تصاعديا كل القيم يحذف 10 بالمئة من القيم العليا و الدنيا.