المحاضرة 04 + التطبيق 04
1- أشكال خاصة بالمتغيرات الكمية المستمرة:
يمكن الاعتماد على قاعدة بيانات موجودة في البرنامج (هناك قواعد البيانات عديد في البرنامج) و هي : "mtcars" و القاعدة مأخوذة سنة 1974 و تخص 32 نوع من السيارات و تتعلق بـ 11 متغير من بينها: كميات جالون الوقود لكل ميل، عدد الأحصنة البخارية، نوع علبة التروس: يدوي أو أوتوماتيكي،...إلخ.
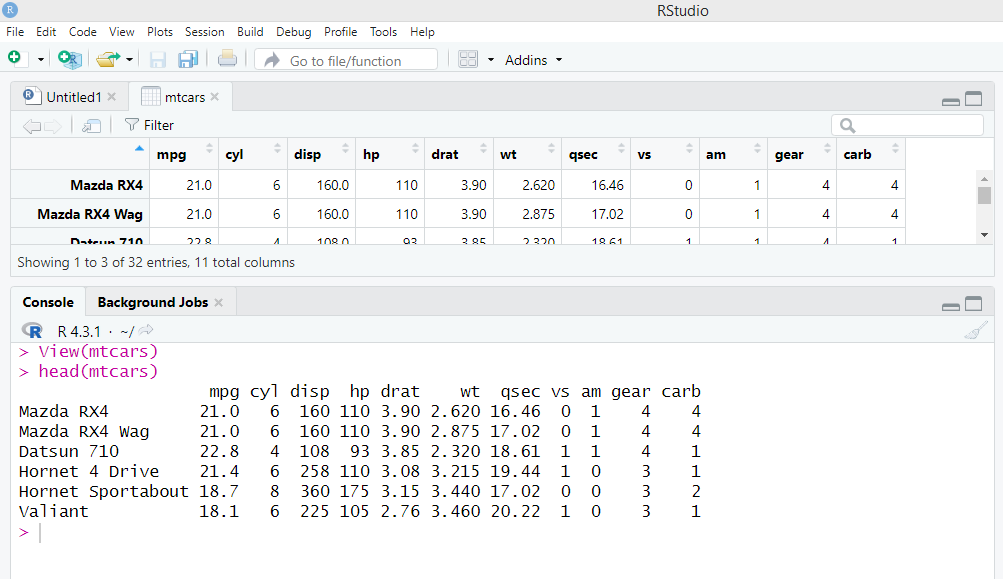
نستدعي قاعدة بيانات "mtcars" بالأمر الأول و الأمر الثاني لإظهار أول 6 أفراد (سيارات):
View(mtcars)
head(mtcars)
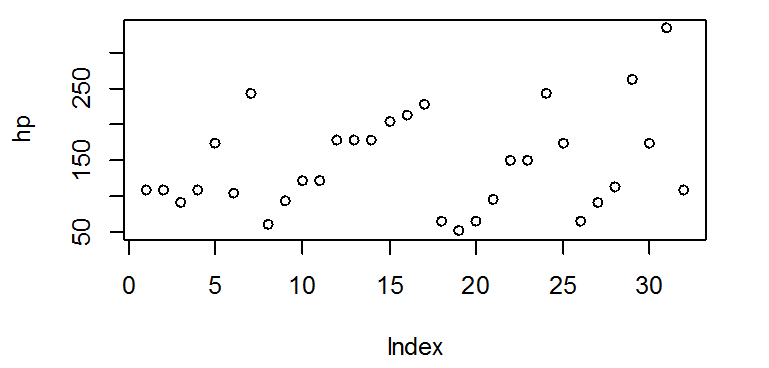
1- الرسم البياني: يعتبر من أبسط الأشكال، أفقيا يرصد عدد المشاهدات (الأفراد) و عموديا قيم المشاهدات، مناسب أكثر للسلاسل الزمنية، نستخرج المتغير الذي نريد تمثيله بيانيا من القاعدة الموجود بها:
hp<-mtcars$hp
plot(hp)
يمكن تعويض النقاط:
|
النوع |
النوع بالانجليزية |
الأمر |
|
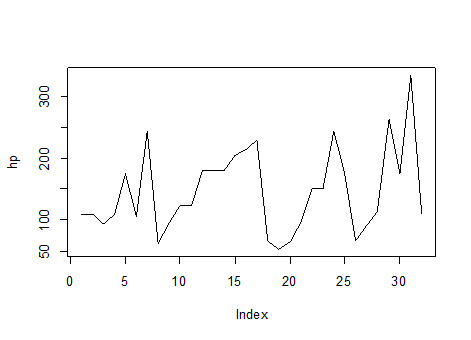
الخط |
line |
plot(hp,type="l") |
|
نقاط و خط |
both |
plot(hp,type="b")/plot(hp,type="o") |
|
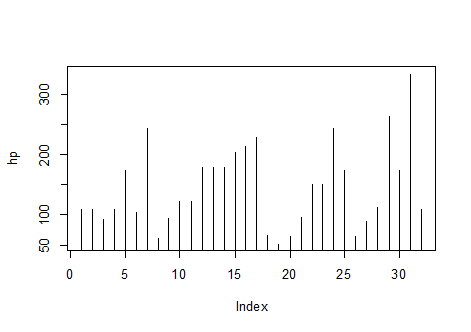
أعمدة أفقية |
horizontal |
plot(hp,type="h") |
|
خطوات |
steps |
plot(hp,type="s") |

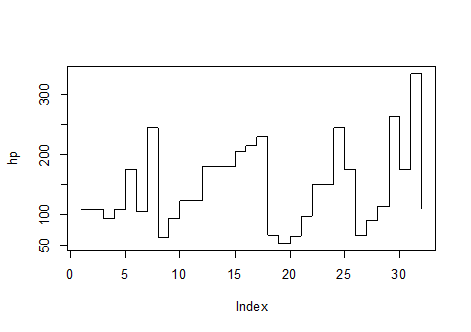
الأمر الكامل (العناصر المهمة) لهذا النوع من الرسوم البيانية، كالتالي:
- شكل علامات المشاهدات: تكون علامات الدائرة افتراضيًا دوائر صغيرة فارغة، يشار إليها بواسطة pch، يمكنك تغييرها بإضافة قيمة pch جديدة في دالة plot قيم Pch 0 إلى 25 صالحة وتعطي عدة رموز مختلفة على الرسم البياني: Pch 0 للمربع، 1 للدائرة، 3 للمثلث، وهكذا.
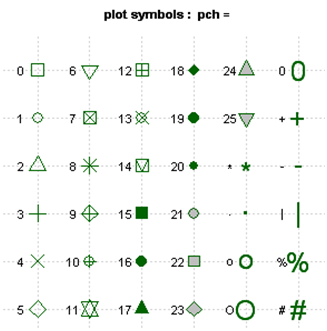
حجم علامات المشاهدات: يمكن التحكم في هذا الجانب من الرسم البياني باستخدام معلمة cex، يمكن ضبط معلمة cex على 0.5 إذا كنت تريد أن تكون العلامات أصغر بنسبة 50٪ و 1.5 إذا كنت تريد أن تكون أكبر بنسبة 50٪.
- لون علامات المشاهدات: يمكن تخصيص العديد من الألوان بالأمر col، يمكن اختيار هذه الألوان من قائمة مقدمة من R،
القائمة نحصل عليها من الأمر colors().
- xlim و ylim: الحدود الدنيا و القصوى للمحور الأفقي x و المحور العمودي y.
- xlab و ylab: تسمية المحور الأفقي x و تسمية المحور العمودي y.
- main: عنوان الرسم.
-تغيير الخطوط: يمكن تعيين عرض الخط باستخدام معلمة lwd.
@اختيارات أخرى في شكل المنحنى البياني
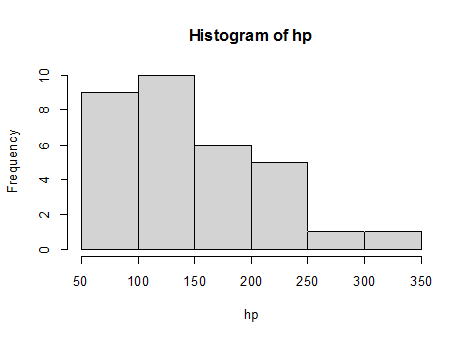
2- المدرج التكراري: مناسب أكثر للمتغير الكمي المتصل، يعتبر كذلك من الأشكال التي يمكن من خلالها معرفة توزيع المشاهدات للمتغير (يستخدم لمعرفة هل المتغير توزيعه طبيعي أم لا)، و كذلك يمكننا من معرفة وجود نقاط شاذة أم لا (أعمدة فارغة –تكرارها معدوم أو شبه معدوم-).
hist(hp)
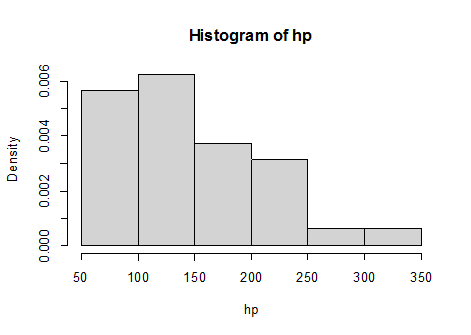
أو إظهار التكرارات بالنسبة المئوية:hist(hp,freq=F)
يمكن رسم دالة الكثافة الاحتمالية على المدرج التكراري بالأمر:
hist(hp,freq=F)
curve(dnorm(x,mean(hp),sd(hp)),add=T)

الملاحظ على الشكل أن هناك ميل سالب (على اليسار) للمتغير hp و من المحتمل أنه لا يتبع التوزيع الطبيعي.
breaks: عدد الفئات.
3- شكل التوزيع الطبيعي: هذا الشكل بالإضافة إلى المدرج التكراري يوضحان بيانيا من أن المتغير توزيعه معتدل أم لا.
qqnorm(hp)
qqline(hp)
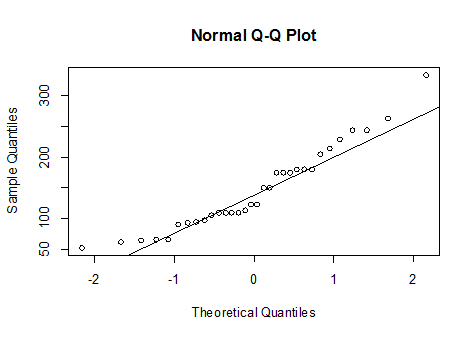
الملاحظ: أن النقاط ليست على الخط و من المحتمل أنها لا تتبع التوزيع الطبيعي.
4- شكل الأعمدة: يناسب أكثر المتغير الفئوي (يعني غير المستمر)،
يشترط التمثيل تكرارات (table) كل قيمة ضمن المتغير.
من الأحسن تعريف المتغير الفئوي أولا (لكي تظهر أسماء فئات المتغير)
ثم رسم الشكل لمتغير am نوع علبة التروس (أتوماتيكي أو يدوي):
am<-factor(am,levels=c(0,1),labels=c("Automatic","Manual"))
barplot(table(am))

ملاحظة: يمكن عمل شكل الأعمدة لأكثر من متغير شرط تساوي عدد الفئات لكل المتغيرات.
@اختيارات أخرى في شكل الأعمدة.
5- شكل القرص: يناسب المتغير الفئوي، و يشترط التمثيل تكرارات (table) كل قيمة ضمن المتغير.
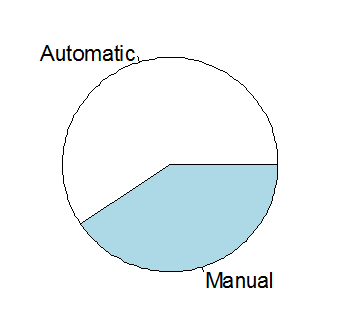
6- شكل الانتشار: يكون بين متغيرين كميين مستمرين، يستعمل كذلك لتمثيل الانحدار البسيط.
plot(hp~mpg)
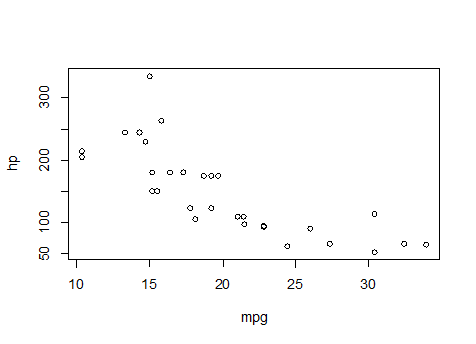
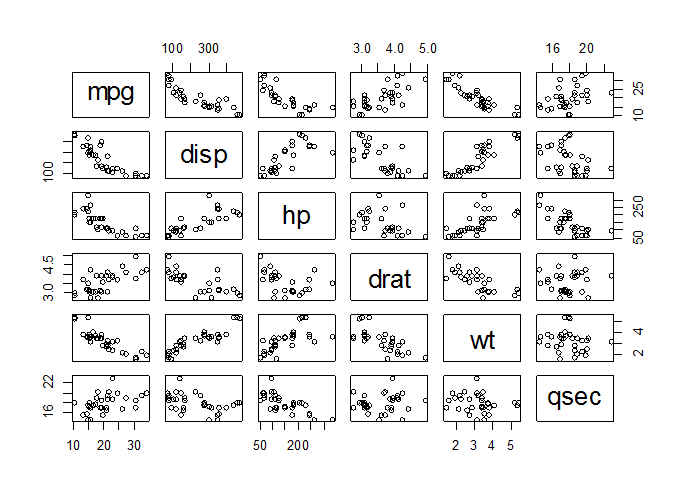
شكل الانتشار لكل متغيرات قاعدة البيانات، كل متغيرين مع بعض مثنى مثنى
(نختار المتغيرات الكمية المتصلة فقط (mpg-disp-hp-drat-wt-qsec)):
pairs(mtcars[,c(1,3:7)])
7- شكل الصندوق: يستعمل الشكل للكشف عن النقاط الشاذة،
حيث تمثل الحافة الأدنى للصندوق الربيع الأول و الحافة العليا للصندوق الربيع الثالث:
boxplot(hp)
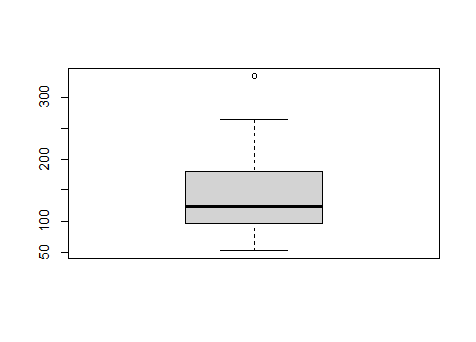
الملاحظ وجود نقطة شاذة واحدة فقط، يمكن العودة للبيانات لمعرفتها.
@اختيارات أخرى في شكل الصندوق.
ملاحظة: يمكن إظهار شكل الصندوق لكل المتغيرات، و ذلك بالأمر الخاص برمز الشعاع لكل المتغيرات
لكن اختلاف وحدات القياس لا يعطينا أشكال أكثر وضوح.
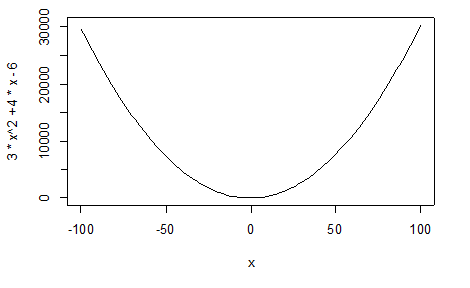
8- رسم منحنى دالة: يمكن رسم أي دالة في أي مجال تعريف نريد، مثال:
3x2- 4x+1
curve(3*x^2+4*x-6,-100,100)
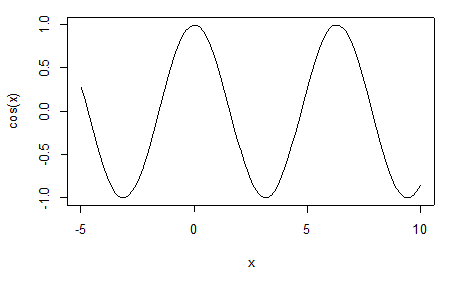
curve(cos(x),-5,10)
9- رسم متغير عشوائي: يمكن للبرنامج أن ينشأ أي متغير عشوائي مهما كان توزيع (شكله)،
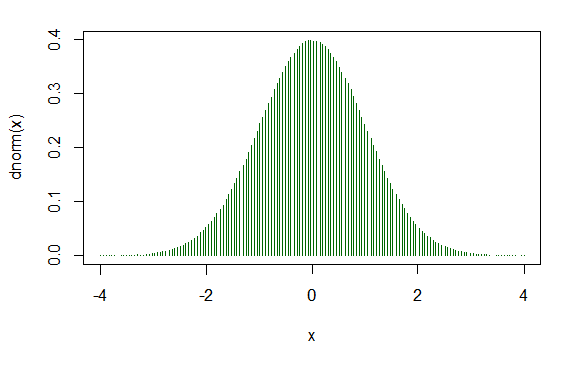
مثال رسم دالة الكثافة الاحتمالية لمتغير عشوائي يتبع توزيع طبيعي:
اسم المتغير: x، توزيعه:طبيعي، مجال الرسم (-4,4)، شكل الرسم: أعمدة متوازية،
عدد المشاهدات: 150 لون الأعمدة: أخضر داكن.
curve(dnorm(x),-4,4,type = "h",n=150,col="darkgreen")
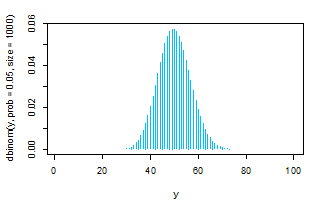
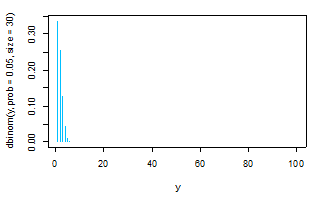
- رسم دالة الكثافة الاحتمالية لمتغير عشوائي يتبع ذي الحدين، لمتغير y يحتوي القيم من 1 إلى 100.
اسم المتغير: y، توزيعه:ذي الحدين، احتمال نجاح التجربة: 0.05، العينة:20،
شكل الرسم: أعمدة متوازية، لون الأعمدة: أخضر داكن. (ثم عند العينات: 100 -1000).
plot(y,dbinom(y,prob=0.05,size=30),type="h",col="deepskyblue")
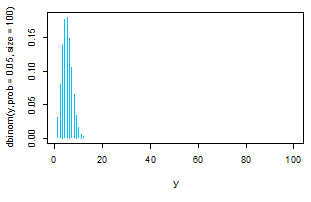
plot(y,dbinom(y,prob=0.05,size=100),type="h",col="deepskyblue")
plot(y,dbinom(y,prob=0.05,size=1000),type="h",col="deepskyblue")